大和尚的因材施教：胖瘦不同体型在雨中行走的最佳策略

naifen102

这几年，许多老师开始尝试“翻转教室”这项新观念——藉由学生在家中看教学影片，老师得以从一成不变的讲课中释放，在课堂上跟学生有更多的互动、讨论，实践真正的因材施教。论语里一则关于因材施教的故事：
1 O' A1 T% d% Z* E% C0 f3 M某天，子路跟冉有先后问了孔子同一个问题：
“听到一个好的道理，就要立刻去实践吗？”
2 R- Y; y8 j9 n. v7 g' G$ O孔子回答子路，别急，你该先想到家里还有父亲与兄长；但却对冉有说，当然，听到就该去实践。在一旁的公西华听了很纳闷，问老师为什么给子路和冉有不同的答案。
8 i4 q! {' a. z孔子说：
9 n  v3 ]9 @- D/ W“冉有个性保守，我要鼓励他更积极；相反地，子路已经够积极了，我得拉他一拉。”《论语．先进》
8 N, w) z* |) \4 F( ?& g5 s根据不同学生的特质，告诉他们不同的答案，才是最理想的老师。这道理，上篇教大家打伞的大和尚也懂。
. m, t3 o. b1 p% Q  q两个徒弟拿伞走了半天，大和尚一行人总算来到个小聚落，聚落里的人生活很清苦，没什么能布施给他们的，大和尚跟徒弟在聚落里的祠堂睡了一晚，隔天一早即动身前往下一个村落。虽然肚子还很饿，但至少天气放晴了，大雨清洗过的草原，翠意盎然，光是看着，就令人比昨天更精神抖擞。然而好景不常，才离开祠堂没一刻钟，乌云彷佛像发现自己睡过头了，迅速从后方赶上，稀哩哗啦地又是一阵大雨。更糟糕的是，背行囊的胖徒弟出发时看到天气好，不小心将伞留在祠堂里。大和尚一行人躲在路旁的草棚底下避雨，讨论该怎么办。
- N2 u6 o4 {$ O/ B“我比较瘦，跑得比较快，不如师父跟大家在这里等着，我回去拿伞。”
一位体态单薄的瘦徒弟自告奋勇，大和尚担心他感冒，但也想不到别的方法，只好目测一下他的身形，再看看棚子外的雨势，掐指算了算。大伙儿送瘦徒弟出发时，最机灵的小徒弟听见大和尚对瘦徒弟说：
“你现在回去，雨会从你身后打来。要是雨势斜到……度，你就全力冲刺，不然，以……的速度走慢一点，比较不会淋湿。”
雨声盖住了大和尚的话，小徒弟听得不是很清楚。过了半响，瘦徒弟还没回来，坐成一圈的大伙儿开始担心起他会不会迷路。胖徒弟霍地站了起来
! W, r; O. }+ M  M7 H' N“我去找他好了。”
“你？不要好了，你那么胖，跑不快，表面积又大，会淋到特别多的雨，等会感冒了。”
“伞是我保管的，本来就该我去找回来才是。”
4 G* r+ E% B5 o+ n; @现在才想到，谁叫你早上只顾着吃。小徒弟心里嘀咕着，但同门师兄弟一场，不好意思说出来。
8 t8 p$ J; `. S2 B* w# `“好吧，那就麻烦你走一遭，看看他到底去哪里了。”
$ L6 z- E* T1 q4 u大和尚又掐指计算了一会儿，接着说
“你随时注意雨势，根据雨打下来的角度，调整你的最佳速度为……。”
大和尚用手杖在地上写了一道复杂的式子，胖徒弟把式子抄在手上，作势吞掉。
4 A4 A, D+ t/ A那是上台前写“人”避免紧张的吧。小徒弟又想吐槽他，等到胖徒弟跑出去后，他才问大和尚：
“师父，同样都是在雨天里奔跑，为什么你给了一道最佳速率的式子给胖师兄，但告诉瘦师兄的却是‘要嘛全力跑，不然慢慢跑’呢？”
$ D! k3 @, ^6 I6 v“因材施教，他们俩个嘛，身材不同。”
5 h$ f; ^/ z/ K! q, p& w大和尚露出微笑，他回答：
5 a5 F2 c9 |' ^, E* ]3 ]“在雨中行走，我们常以为全力奔跑，降低在雨中停留的时间，可以淋到最少的雨。但事实上，跑得越快，雨势相对会变得更水平，身体受雨的面积因此增加，脸上、胸膛，都会被雨淋到。因为‘被淋到的雨’同时跟‘雨中停留时间’和‘身体受雨面积’都成正比，最小化前者，却大幅增加了后者，反而不一定是最佳结果。”
大和尚又拿起手杖，在湿掉的泥土地上画了个图形。
( S" C# b% [$ ~

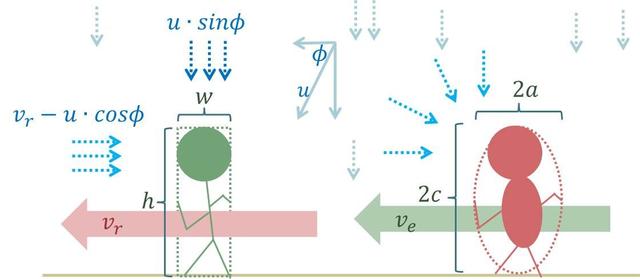
大和尚的因材施教：胖瘦不同体型在雨中行走的最佳策略

制图/赖以威
  D3 K% X+ t+ b9 b0 n- f) i“瘦徒儿的身高h，身宽w，他的侧面可以用一个长方形来近似。假设雨势跟水平夹角是φ，瘦徒儿奔跑的速度是vr，那么，单位时间内，长方形的高所受到的雨势是：h?(vr -u?cos?)/vr
, |0 ^3 o9 q) a( j长方形的宽被雨淋到的量则是：(w?u?sin?)/vr
两个相加，整理后得到：h+u(w?sin?-h?cos?)/vr
从这个式子里可以看到，要是w?sin?-h?cos?>0，表示第二项是正的，这时候提升vr跑越快越好，因为第二项会减少。但要是 w?sin?-h?cos?<0，则跑太快，反而第二项负的会变小，表示会淋到更多雨。这时，最佳策略就是‘像风一样’，保持同等于雨势水平分量的奔跑速度，抵消雨的水平速度。这么一来，只有头顶、肩膀、以瘦徒儿的高鼻子会湿。这么一说，他倒是很像那个香港艺人，唱《风一样的男子》的……”
4 R& g; Y. Z2 K0 `/ j1 V大和尚自己傻笑了起来。
数学无所不在小徒弟不理师父无聊的笑点，蹲下来低头钻研泥土上的画。除了长方形之外，师父还画了另一个椭圆形的人，那应该就是胖师兄吧，可是，这两者之间有甚么差异呢？站着的大和尚回答，一句句解释从小徒弟头上落下来:
- c. G1 w) L% ?% q# U  q$ a/ T“椭圆形的胖徒弟，就算雨是垂直的，他的胸口跟鲔鱼肚都还是会被淋湿哦。”
“原来是近似于身体的几何图形不同啊……”
“是啊，假设胖徒儿的身材是一个椭圆形，用方程式表示为：x2/a2 +y2/c2 =1
其他的计算方式就差不多，一样算出他的表面积在不同奔跑速度影响下，被雨淋到的份量，再利用微分取极值。可以得到：ve=u?cos?+(a/c) 2?tan??u?sin?这样的结果。有趣的是啊……”
; I, p- D. D. S$ m, H0 T  ^) J' K大和尚讲得兴起，不管在一旁开始推导的小徒弟，或早就被催眠到睡着的其他徒儿，自顾自地说下去，“这式子告诉我们，要是胖徒儿的肚子越大，个头越小，就得跑得更快。这难道是上天对体型的歧视吗……”
过了大半刻，好不容易雨停了，胖徒弟跟瘦徒弟才一起回来。当他们的身影同时出现在草棚前时，还在算微分的小徒弟抬头一看，背对阳光的他们，看起来就像是一个10。小徒弟顿然领悟，数学这东西，真是无所不在啊。
  M# t% I' Y  D- m! Y. ^( y果壳相关小组死理性派

ntb

首先，我们假设真空中有一个球形的和尚。。。