划龙舟,不可或缺的角色是负责指挥的鼓手。随着鼓点的节奏,桨手们整齐划一的动作本身就是一种享受;而整个船队的高度一致,不但是大部分船队眼中的“常识”,甚至成为了诸如管理学等领域的著名比喻。但是……如此整齐划一,真的是最快的方式吗?5 B7 x& x7 u# u9 E6 [
International-Dragon-Boat-Race2.jpg
 上海国际龙舟节的龙舟比赛,可以看到所有队伍的所有桨手都是同步划桨的。图片来源:scandasia.com/ x6 U0 M3 q8 e" e/ {
上海国际龙舟节的龙舟比赛,可以看到所有队伍的所有桨手都是同步划桨的。图片来源:scandasia.com/ x6 U0 M3 q8 e" e/ {
其实一直有另一种观点在偷偷流传:每个划桨者各自错开的话效果会更好,因为这样的速度更均匀,更节能。其原理和长跑运动员大部分距离要保持匀速基本相同。事实上,磷虾的游泳法就是异步的……的确,在几个案例里,尝试异步划桨的队伍没有取得成功,但是个案不足为据,这要靠控制变量对比实验才能说明问题——而2013年,可爱的荷兰研究者真的这么做了。. k/ e5 ? e4 u; h" L
龙舟物理学竞技龙舟的目的是用最短的时间抵达目的地,这就要划桨者尽可能增大功率输出、减少损失。而划船时的损失不光在于阻力本身,还有一个因素是船体速度的波动——波动越小越节能。
" y" n2 V: G1 E$ X$ f& l3 v船受到的阻力有四种:船体和水接触的阻力,船体和空气接触的阻力,湍流带来的能量耗损,以及划开水面产生波浪带来的能量耗损。一般的船主要耗损是波浪,但竞技龙舟的船体经过设计,使得接触阻力占主导地位(80%以上)。. P; N: p& X( {6 M3 z: h4 i0 k
接触阻力和速度的平方成正比——也就是R = av^2,a是系数。而为了维持稳定速度,所施加的力就应该和阻力相当,所施加的功率就是P = F·v = av^3,功率和船速三次方成正比。 o- O: p% r D7 I, I5 i5 j
假如一艘船先用4米每秒的速度划一分钟,再用6米每秒的速度划一分钟,一共前进了600米,为了方便假设a = 1(kg/m),总功就是6 v0 L8 E, K4 O- ]) s
W = 60 × 4^3 + 60 × 6^3 = 16800(J)
) ?. `' g0 S+ q; e& X而假如两分钟都是5米每秒,总功就是
! d" K& o5 l; k( g" M$ TW = 60 × 5^3 + 60 × 5^3 = 15000(J)
: E" V! J% R/ A0 A8 x# A4 m显然匀速更节能。
( c! G( Z- C7 n
basics_5.gif
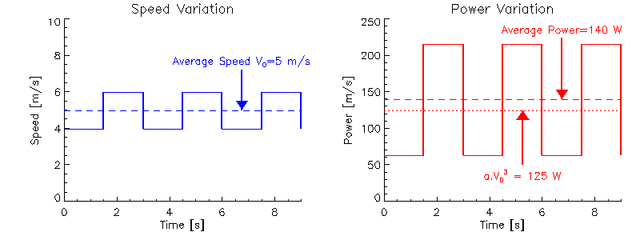 速度有波动时的功率变化,因为公式里的立方的缘故使得平均功率上升。图片来源:http://www.atm.ox.ac.uk/rowing/physics/2 j- a$ c7 c1 ~" m
速度有波动时的功率变化,因为公式里的立方的缘故使得平均功率上升。图片来源:http://www.atm.ox.ac.uk/rowing/physics/2 j- a$ c7 c1 ~" m
由于阻力只取决于船体对水的相对速度,而不取决于质心对水的相对速度,因此这个分析对于一桨之内的速度变化同样适用。之所以一桨之内速度有变化,一方面是因为推力不均匀,另一方面也是因为划桨时桨手的重心移动、对船体施加了反作用力。5 W; A2 y, v+ P( v/ v. a
basics_4.gif
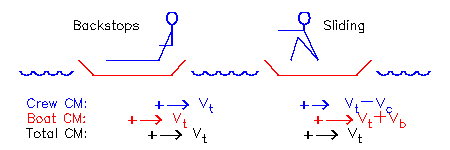 划桨带来的重心移动。图片来源:http://www.atm.ox.ac.uk/rowing/physics/$ J9 h* R o$ z/ m
划桨带来的重心移动。图片来源:http://www.atm.ox.ac.uk/rowing/physics/$ J9 h* R o$ z/ m
如何匀速?速度波动这个因素损失了多少呢?实测表明,竞技赛艇的速度效率在0.94-0.95之间——也就是约94%-95%的能量用来克服“正常”的阻力,还有5%-6%的能量浪费在了速度的波动上。在竞技比赛中,这可不是个微不足道的数字。事实上,早在1883年,就有英国工程师设计了一种“滑架”(sliding rigger),让座位和桨架一起滑动,消除桨手的重心移动。由于材料问题这一设计当时没有投入使用,但是到了1981年,德国人彼得·科尔比(Peter Kolbe)凭借一艘滑架艇一举夺得世界赛艇锦标赛冠军。接下来的两年里滑架如此成功,以至于1983年委员会决定将其禁用。# ~- q# I. s* g
riggerHeadSeatedView.jpg

, y. N$ O# z$ ~% X& J. n
riggerSideView180.jpg
 一种滑架。图片来源:slidingrigger.net2 g V' Q5 x% u9 k- Q6 M h
一种滑架。图片来源:slidingrigger.net2 g V' Q5 x% u9 k- Q6 M h
机械外援不能用,但还有别的办法。大家错开划的话,不同人的节奏相互抵消,理论上速度就会更均匀。但是,完全均匀错开会给桨手们带来很大的困扰。20世纪20年代,英国桨手尝试过八人四相策略(每人的划桨周期比前一人提前四分之一),而六人赛艇队则是三相(每人的划桨周期比前一人提前三分之一)。这一异想天开的计划不但饱受报纸批评,实际上也没有产生什么成效——因为精确维持这个差异实在太难了,很容易乱套。1985年,生物力学研究者提出了所谓哈肯-凯尔索-本茨模型(HKB Model),用来讨论多人协调时的自组织现象;按照这个模型,在赛艇的场景下,完全同步是最稳定的(很符合直觉),相位正好相反的划法次之,英国人尝试的提前三分之一和四分之一都不稳定。传统划桨既然是完全同步,那我们就该尝试一下每两个人完全错开的反相划桨法。9 T) H. Q' `. W0 j
根据理论计算,成对桨手完全错开划桨的话,在2000米八人赛艇里足以赢得一个船身(3.0秒)的优势。不过这个理论计算没有考虑错开划桨对桨手的影响——毕竟大家一直接受的都是同步训练,异步划桨本身稳定性就差一些,划起来的感觉也不一样,都可能影响发挥。那么两种划法到底谁好,还是要看实验决定。
% T5 |& ^ {8 }2 P% Q+ t* h实验说了算
journal.pone.0054996.g001.png
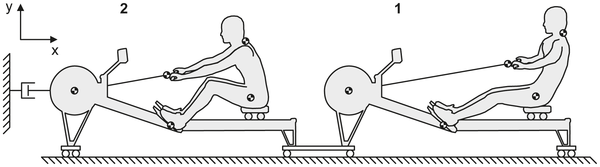 实验设计示意图。" D* Z Z+ I9 d* B' r! q7 k
实验设计示意图。" D* Z Z+ I9 d* B' r! q7 k
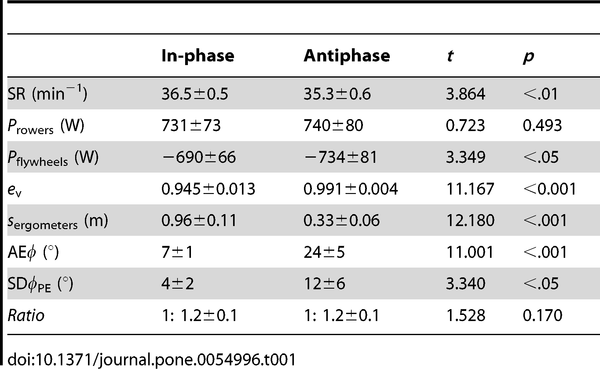
荷兰人的实验结果在2013年发表在PLOS ONE上。他们招募了18位身高体重基本相当的富有经验的男性桨手(约有五年左右俱乐部级比赛经历),两人一组在专业级划桨训练机上进行测试,并在上面加装额外的伺服器用于模拟速度波动带来的损失。每组先进行5分钟的慢速同步划桨和异步划桨作为热身,再全速(每分钟36桨)各划两分钟作为测试。结果有一组在全速划的过程中不自觉从异步切换到了同步,这一组数据被排除,剩下的八组结果如下:
* ^. R- N% I% U* H
journal.pone.0054996.t001.png
 , x3 q6 g$ a/ L' N3 U+ Y; Q
, x3 q6 g$ a/ L' N3 U+ Y; Q
可以看到,在划桨者的能量输出(Prower)上,两种方式没有显著差异。但是,传递给划桨机——也就是龙舟的能量却有显著的差异,错开划的办法高出了差不多44瓦。对应地,速度效率也从同步的0.945提升到了0.991,4.6%的提升已经逼近了5%-6%的理论值。每一桨周期里,同步法的划桨机总共移动了0.96米的路程(相当于实际比赛时重心前后移动而产生的“额外”路程),而异步法只移动了0.33米。
7 q j' a( T" x* x; l) S当然,异步法的不稳定也付出了代价:AEφ用来衡量实际划桨者和理论周期的偏离,异步划桨者距离理论周期的偏差要大得多。但即便有这个不利因素,异步法的表现还是强于同步法。当然我们也不能忘记那对不小心划乱了的倒霉鬼……(他们是所有划桨者中经验最少的,之前也没有一同训练过,这算是原因之一吧。)+ B/ ~- H1 h( y* ?/ V7 P
那么,这个实验能否外推到现实中的龙舟比赛呢?假如龙舟只有两个人、每个人只有一把桨,那么显然异步法是行不通的,因为船会左右晃动。但现实中龙舟人数很多,不存在这样的问题。异步划桨需要更长的船以免桨手撞上,八人船需要额外长70厘米,好在船的长度对阻力的影响微乎其微。最后,异步划桨是否会产生额外的不良湍流还是未知数;但无论如何,看起来总是值得尝试的。打算参加赛龙舟的读者,下次可以试着训练一下异步划桨方式——不过其产生的后果,无论胜利失败,本文作者概不负责。
( \; H4 B1 T- [# \8 q7 q7 D' n参考文献:Anouk J. de Brouwer, Harjo J. de Poel, Mathijs J. Hofmijster(2013). Don't Rock the Boat: How Antiphase Crew Coordination Affects Rowing. PLOS ONE, DOI:10.1371/journal.pone.0054996南通0 |  苏公网安备 32060202000307号 © 2001-2019 0513.org All Right Reserved.
苏公网安备 32060202000307号 © 2001-2019 0513.org All Right Reserved.