π里包含了所有可能的数字组合吗？

beiju8125

在《疑犯追踪》S02E11里，“宅总”哈罗德·芬奇说了这样一段话：
( C  @; w" v5 Z9 M& J- @

poi.jpg

% u) v2 w$ Z: H, Y! U/ G8 ~“π，圆周长与其直径之比，这是开始。后面一直有，无穷无尽。永不重复。就是说在这串数字中，包含每种可能的组合。你的生日，储物柜密码，你的社保号码，都在其中某处。如果把这些数字转换为字母，就能得到所有的单词，无数种组合。你婴儿时发出的第一个音节，你心上人的名字，你一辈子从始至终的故事，我们做过或说过的每件事，宇宙中所有无限的可能，都在这个简单的圆中。用这些信息做什么，它有什么用，取决于你们。”
) Q$ f+ ]/ F& Y" q# B* e5 T很多观众看到这一段之后十分感动，还有人感慨：为什么我们的数学老师没有这么教我们呢？
之所以我们的老师不讲，是因为这段话在数学上是不对的。
- P, f' `7 J5 ]* z+ R6 G6 d无理宅总的前两句话正确地描述了π的一个属性：无穷无尽且永不重复——换句话说，π是个“无限不循环小数”，也就是“无理数”。
但是，一个无理数并不一定能包含“每种可能的数字组合”。
举个简单的反例：0.909009000900009000009……
（除非特别声明，所有数字都是10进制的，下同。）
; ^% Y9 j. g( [! h这个数的特点是，两个“9”之间的距离会越来越长，每次多一个0，直到无限。它是无穷无尽的，也是不循环的，因此是无理的；但别说“每种可能的数字组合”了，它连0到9这十个数字都凑不齐呢！
5 H- F* o6 o9 n* y5 c合取包含所有数字组合的数，叫做“合取数”。无理数并不都是合取数。
一个典型的合取数是这样的：0.10200300040000500000600……000110000000000012000……
在越来越长的0串中间，夹杂着从1开始的所有自然数，直到无限。既然包含了所有自然数，当然也就包含了所有的数字组合。
5 ?  V9 [0 [+ f# G+ v正规但是写这么多0，多费纸费电啊。如果把这些零去掉呢？
$ Q+ F. N* u5 o+ t3 \得到的数就是这样：0.123456789101112131415……
5 y9 x' B$ o% b' x7 U7 ^! _这个数不但是合取的，还是“正规”的——从0到9的每一个数字，出现的频率都趋向于一样的值。
随机如果我们再进一步，连生成规律都不要了，而是用某种真随机生成器（比如哥本哈根解释下的量子随机性）造出一个每位都随机的数，那么它当然就是“随机”的了——不光每一个数字的长期频率趋于一致，任何位置出现的概率也都一样。
那pi是什么？非常遗憾的是，目前为止我们只证明了pi是个无理数。pi是合取（包含所有可能）的吗？是正规（所有数字出现频率趋于一致）的吗？是随机（每一位上的数字都随机）的吗？
答案是：全都不知道。
我们很容易构造出一个合取数或者正规数，甚至能证明“几乎所有”实数都是合取而且正规的，但是随便拿一个具体的数字，要想判断它是否合取、是否正规，却极其困难。我们甚至都不知道pi里面是不是有无限个数字2。至于随机？别跟我提什么随机。
合取数和正规数有另一个有趣的性质：和进制有关。有个常数叫斯通汉姆数（Stoneham number），在二进制、四进制、八进制……下已经证明全都是正规的了，可是在六进制下却能证明它不是正规的。如果一个数在任何进制下都正规，可以称之为“绝对正规”。不幸的是，pi在任何进制下都没能证明正规——离得最近的是2，有论文证明，假如某个猜想是对的，那么pi就是二进制正规；但那个猜想本身也只是“很可能正确”，还没有得到严格证明。
6 n- e3 ]! ~+ \( d当然，我们都已经计算出pi的几百亿位了，可以看看它们的分布来猜规律；也可以通过一些其他数学方法拐弯抹角地试图推断。从已知事实来看，pi和正规性吻合得非常之好，换做任何别的人文、社科、自然科学，都可以当做定论来用了，因此几乎所有人都“觉得”它该是正规的。可惜，这是数学，数学是靠证明说话的，只要拿不出证明，数学家就不能安心睡好觉。
2 z3 m0 ?7 a( J- s& V

pseudo random.png

平面上的一个随机行走路线，每一步随机选择上下左右四个方向之一。本组行走路线图片来自David H. Bailey and Jonathan Borwein，下同。

pi 1.png

用四进制pi前1000亿位生成的行走路线，0123分别对应上下左右。看起来和随机的很像。但只是看起来。

champernowne.png

用四进制詹帕诺尼常数（Champernowne's number）生成的行走路线。这个常数是正规的，但显然一点儿都不随机。

stoneham 4.png

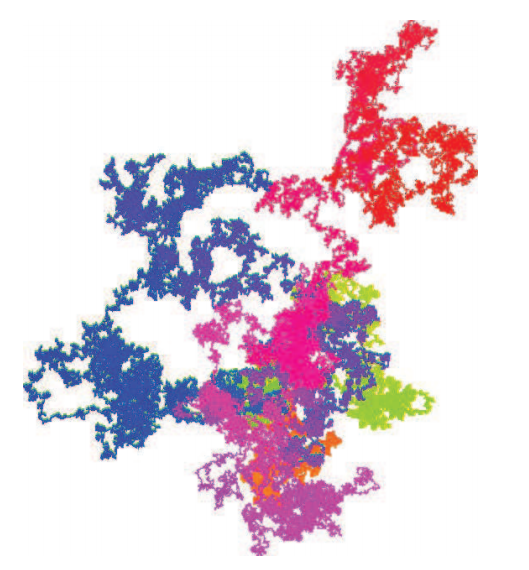四进制斯通汉姆数生成的行走路线。它是正规的，看起来也很随机。
6 v& ^3 p! G! E! S5 [. @8 F" T" E

stoneham 3.png

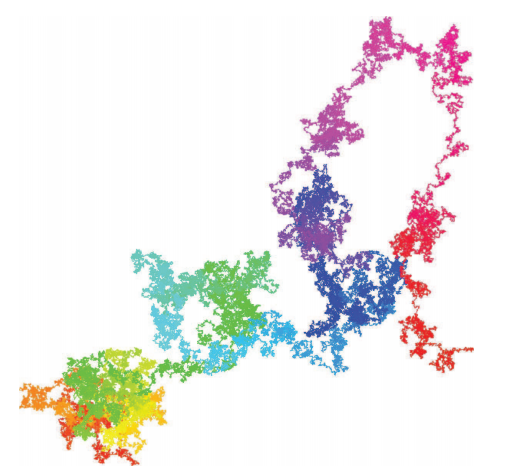三进制斯通汉姆数生成的行走路线。我们不知道它是否正规，但至少看起来和随机很像。

stoneham 6.png

六进制斯通汉姆数生成的行走路线。它不正规，所以……也完全不随机。就是这么一条儿。
为什么要在乎这些细节呢？这篇文章不是为了批评《疑犯追踪》这部剧，事实上看到这一幕的时候我还非常高兴：影视剧里到处都是坏掉的理化生，而坏掉的人文社科干脆就是某些作品的主干——但现在终于出现了（哪怕是坏掉的）数学了！数学至少有了存在感！
8 [# W; X. ?$ `但是这文章又必须要写，因为编剧在写这个段子的时候违反了基本的数学精神。其一，数学靠证明说话，哪怕pi距离“包含所有可能序列”离得再近，哪怕每一个人试过的每一个数字序列都能在它里面找到，在得到证明之前你也不能这么说；其二，数学是一个严密的逻辑体系，就算pi真的包含了所有可能性，你也不能说“因为它是无理数所以它是合取数”，这个推论本身的逻辑是错的。哪怕结果蒙对了，也不能为此放过错误的过程，否则整个数学体系就无法存在。
0 E+ b" o8 M4 Y& b2 |目前看来，pi“应该”是正规和合取的。如果让我打赌，我当然押“包含所有序列”一边；如果我在现实生活中用到了pi，我也会把它当做合取数和正规数那样用。甚至可以说，我“相信”pi是正规的：如果有人告诉我它不正规，我第一反应肯定是不接受；如果计算发现pi从第一万亿位开始变成了9090090009……，我没准都会开始怀疑宇宙的真实性——但是，只要没有出现证明，我就不能言之凿凿对你说：“pi里面包含了所有可能的数字组合”，更不能用似是而非的推论来支持这个说法。经验、审美甚至信仰，在数学里，都敌不过薄薄的一纸证明。
# c7 u3 l- J% `7 L/ z+ }& m4 Q9 K) V其实死理性派也有情怀，只不过往往用在了奇怪的地方。
P.S. 下面是一些和pi相关的网页：
有个工具能在pi的前2亿位里搜索任何一个数。范围里搜到任一八位数生日的概率是86%。
WolframAlpha整理了一些关于pi的有（wu）趣（liao）小知识。
, I' F. C, G9 h+ L$ l3 N% O; T这个网页上列举了pi的前100万位。
基于pi“很可能有”的合取性，有人半开玩笑地设计了一套文件系统“πfs”，你的所有的数据都（很可能）存在pi的某一个地方，只要找到那个地方就好了。
' t! A( b# ]1 W, p+ k  w6 J参考文献

David H. Bailey and Jonathan Borwein. Pi Day Is Upon Us Again and We Still Do Not Know if Pi Is Normal.  American Mathematical Monthly, Mar 2014
1 v9 ^7 B* x5 C

kakatlj

好厉害啊没懂…………

皇甫小二郎

数学有了存在感，呵呵