直觉，到底管用不管用？

快快乐

“应该是这样吧”。
5 U1 h! J) X( ]3 m" S+ m许多时候我们遇到不懂的事情，常习惯就这么歪头两秒钟，然后，彷佛答案卡在脑袋里面一样，摇一摇，答案噗通一声就掉出来了。
. `% t, n  F  m2 e/ `) w* A% l- M6 B7 B有人称这是直觉。
+ M4 U' Z$ X. r( @然而，很遗憾地，大多数人的直觉都不是很准，不然就不会那么多人在彩票选号时面带微笑，还善良地想着要捐出一半头彩。
' R( y2 J' A. j, H$ B- O6 k) Z8 ]要是理性点，应该会很忧心忡忡地想着
* I6 T+ Z( a( ?50元花下去，中三码的概率仅有1.78%，好低。
六码全中的头彩概率更是低到7.15亿分之一，比每天车祸致死的概率5.25亿分之一还低，唉。
就算不讲容易让人不理性的彩票，直觉在许多时候也经不起数学的检验。更正确一点的说法是，直觉本来就不大准，只是这世界并没有太多事情能搞清楚对错，所以不容易察觉到直觉到底有多不准。好比你觉得隔壁同学暗恋你，因为她下课常问你要不要一起去商店，但事实上她只是单纯想找人陪，可是在告白之前，你无法确认这件事情的真相。
更可悲的是，就算告白成功了，你还是无法确认她是否真的爱你。
3 w$ z- x5 l$ s4 R4 s' s( R$ x听不懂吗？没关系，再长大一点就懂了。
2 h) B0 H: R9 n. X今天，我们藉由简单的数学统计，让大家实际看看，直觉跟事实间的差距，恐怕比台湾蓝绿两党之间的差距还大。后者至少还有“无能”、“贪污”、“让老百姓气到高血压”等等诸多共同点…嗯，他们其实蛮像的，我似乎举错例子了。
& ^: k9 J" u( u. p9 \' z4 h" ^直觉 vs. 数学翻开存折，看看最左边的数字，将这个数字称为“首位数”，一百多万的首位数是1，六千多元的首位数是6，八十几块的首位数即是8。现在，请用直觉判断，全台湾两千三百万人的存款金额首位数，1~9各个数字出现的概率各自是多少呢？
4 Z- K3 s+ R: G均匀分布，每个数字出现的概率皆是1/9。
/ x% P' \' Z+ V6 ?# @+ d( t许多人的直觉应该此刻在脑海里吶喊着这个答案，还带点不屑。
  W. {% }' n4 z要是顺从直觉，按照这个逻辑继续推理下去，使用欧元的人的存款金额首位数，日本人的日币存款金额首位数，每个数字出现的概率应该也都是1/9的均匀分布。没理由这项统计数字在台湾是均匀分布，到欧洲或日本就会改变，大家理当都该一样。
现在，当我们假设有9个人，户头里各自有100、200…900元新台币，符合均匀分布。
要是银行忽然将他们的存款改以日币或欧元计算，会得到下表。

直觉，到底管用不管用？

可以看见，首位数1从出现一次，大幅增加到三与四次，首位数9则消失在表格中。
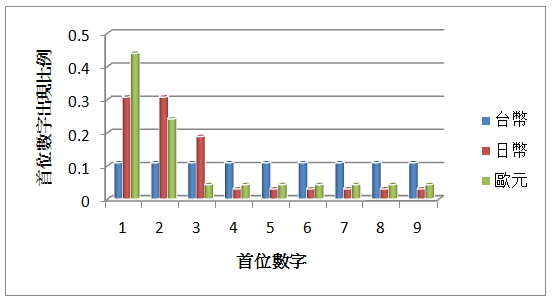
考虑更一般的状况，可以得到下面的统计分析图。当台币换算成欧元或日币时，首位数数字小的出现概率都比较高。

直觉，到底管用不管用？

至此，可以宣告直觉失败，输给了所谓的“本福特定律Benford’s Law”：以自然形式出的数字，首位数是1的概率约30%，2的概率是17.6%，依序递减，首位数是8与9的概率各自仅有5.1%与4.6%。
本福特定律是哪招
/ |! i( V  r6 U要解释这种不直觉的递减现象，我们得先提一个生活中的例子。
想象一条长条状的蛋糕，蛋糕上不同区域，有不同的装饰：有些地方是草莓、有些地方是樱桃、还有些地方是肉桂跟大蒜。
* G4 S& V" M: N1 e6 f要是有四人想分这条蛋糕，而且每种装饰都想吃到，最常见的作法，就是先将蛋糕由上往下，切成许多片，每一片的大小符合每个人能拿到的比例，切完后依序1、2、3、4、1、2、3、4…等分。每个人再根据自己的编号，周期性地挑出属于自己的蛋糕。如同下图。

直觉，到底管用不管用？

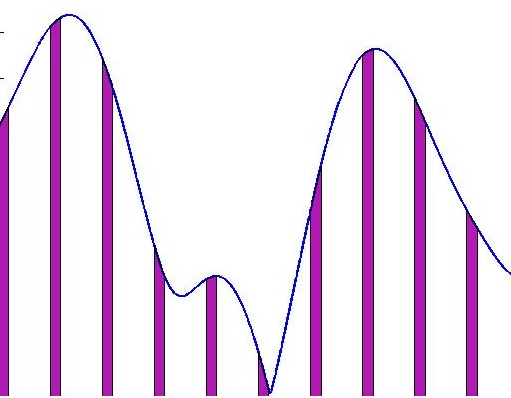
! U  \: y; j& r4 r' p上图就是其中一人的切法。在每隔一段距离，切下等宽的一部份。可以确保每个人拿到他该拿到的比例，且各种装饰都能拿到。我们称这种为“理想蛋糕分法”。
) e' h% @2 K! r& D  v2 l1 M回到首位数的问题。
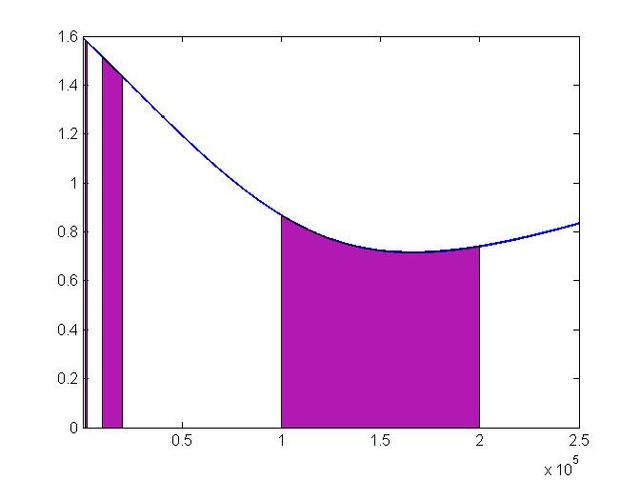
' P  z% V6 _, r4 d要是统计全台湾的人银行存款，可以画出存款的统计分布图，我们用下面这张示意图表示。

直觉，到底管用不管用？

存款首位数为1的区域我们用紫色表示。要是将整个曲线想成一条蛋糕，切下的紫色区域起先是一条细细的“1”，过了2-9后，再来一块粗一点的“10-19”，这次得隔久一点，过了0-99，才会再出现更粗的“10-19”。然后，得一直等到“1000-1999”。
$ X* k& C7 P; I' T切下的区域分别是1、10、100、1000……切的间隔是8、80、800……。
换句话说，依据不同首位数的蛋糕切法，在不同间隔间，切下大小不同的面积，不是刚才说的“理想蛋糕分法”。可能，落在300-500的樱桃就这么没了。
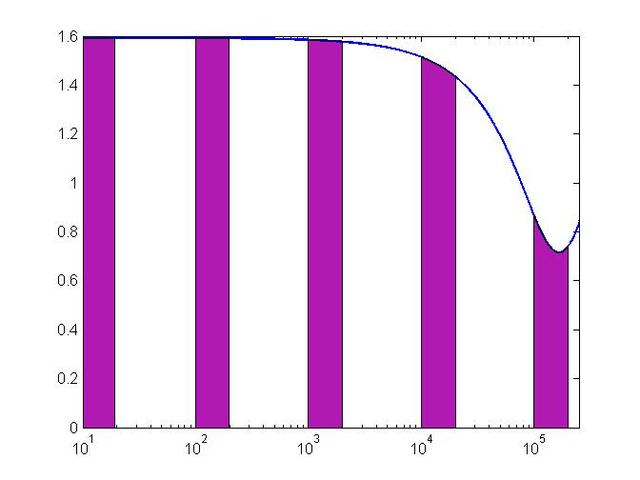
' o1 q4 r7 P5 w, `9 T2 F不过，要是将x轴的金额取对数(log)，就会得到下面这张图。

直觉，到底管用不管用？

方才所说的“理想蛋糕分法”——等间隔切下同样大小的区域，在此重现了。
因为是等间隔，不同区域的装饰都能拿到，以取样的角度来，就是取下来的部分能够充分反映原来曲线的特性。
有趣的是，在对数转换后，首位数为1切下来的面积所占比例是log102- log101=log2-30%，首位数是2的比例则是log103- log102=log10(3/2)-17.6%，归纳出首位数为x时，所占比例为log10(1+1/x)。
9 ]2 L2 z; C, X1 |3 T' D* t这才是真正的首位数分布。
# U8 s& r/ a9 g5 M. H$ ?# }. @- E9 f回到刚刚不同币值的问题，如果假设新台币的存款首位数分布是依据本福特定律时，换算成欧元跟日币后，可以得到下图。
/ F. v9 y' O/ }! r. I/ W  b7 H

直觉，到底管用不管用？

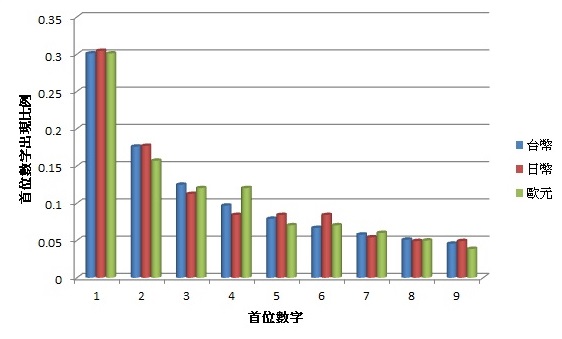
" m2 q2 f5 i4 {5 [9 k/ L% j可以看见，换算到不同货币后，趋势依然相似，大致依然符合本福特定律。终于，我们看到log离家出走，离开了数学课本。
" `# L1 |7 w3 \+ C数学界的捉虫达人，本福特定律只要是自然产生的数据，且数据涵盖范围很大，首位数分布即会符合本福特定律。
. x6 A9 Y/ d7 l2 a4 P9 e因此，本福特定律相当具有实际用途。好比，统计公司一年的各种报账款项，便会看见本福特定律的存在。政府或会计师即可反过来利用本福特定律，审核公司报账是否诚实，如果不符合本福特定律，可能就有问题了。
奈何我无法拿各级政府，或首长特别费的资料实际测试一下本福特定律的威力(也怕测出来发现不符合，大家反而会说“这不是理所当然吗”)，只好拿2012“总统”大选各乡镇的投票结果来看：
( T. j# ]4 j1 c! g$ A+ @

直觉，到底管用不管用？

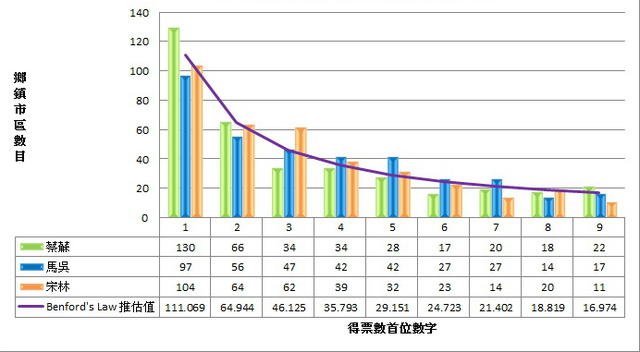
0 z# E- l* U+ h1 u& O) t结果相当符合本福特定律，这告诉我们，要么“总统”大选没作票，不然就是作票的人精通本福特定律。
" |1 f  Y& f! r9 m# `: z从一开始就说，别相信直觉了嘛。
参考文献
0 A) u# `  B8 F

        R. M. Fewster, “A simple explanation of Benford’s law,” the American Statistician, vol. 63, no. 1, pp. 26-32, 2009, Nov.
6 D: h9 Y& J4 U. r1 v' o       
7 R# o+ |& l+ H! E/ k

沙漠之鱼

当我和别人表白的时候，直觉认为会被拒的时候，我的直觉都是对的！直觉认为不会被拒的时候，也是对的！但只是对方不好意思说出来拒绝的话而已。。。。

zjhluchaodong

作者写的实在是很难懂，又跑到别的地方看了看才明白。作者是不是凭借直觉认为，读者们可以轻易看懂没有标注xy轴单位是什么的图XD
我觉得，要想把科普文章写的人人都可以看明白，还是有一定难度的。
作者加油！

盆景园

其实妹子只是觉得..恩..这个家伙..应该还算安全吧..也不算太无聊.....叫上他一起去好了...然后几次之后觉得..唉~~带着这个家伙还蛮方便的......然后...你去告白了....事实上..妹子确从没那么想过= =....55555555555555..........