我从未见过一款富有数学元素的游戏，能够这么美

黄泥山

本文作者:娄大江
                    不知你是否曾沉浸于斐波那契螺旋线的迷幻？不知你是否曾迷失于彭罗斯三角的神秘？不知你是否曾陶醉于正多边形的优雅？
当这一切与《纪念碑谷 2》结合起来的时候，你会惊叹，原来一款富有数学元素的游戏也能让人如此喜爱。
& O6 F4 G- b/ W) ^9 b* f

我从未见过一款富有数学元素的游戏，能够这么美

) f: ]0 m  Q0 @+ r* R) A0 j《纪念碑谷 2》的设计风格简洁干净，没有冗余的装饰，每一个关卡都可以截图做成一张壁纸。其沿袭了一代中的视错觉、不可能几何等经典设计，而其添加的新元素——“树”的设计更是点睛之笔，令玩家难以忘怀。
( S( F- W; Q7 g8 p7 a7 A那么除此之外，《纪念碑谷2》的画面里还隐藏着哪些玄机，让人对这个小世界欲罢不能呢？
不可能图形，谜题从此而来《纪念碑谷》中的很多谜题设计都来源于不可能图形，这种视觉欺骗往往让人感到不可思议。最基础的，也是出现很多次的便是彭罗斯三角形。
彭罗斯三角形被称为“最纯粹形式的不可能”，它将三个不同角度的三角顶角整合为一个整体，因而本应是一个平面的面发生了扭转，而这样的三角形在三维世界是不可能存在的。
% ~3 w- p9 c7 p5 Y/ n

我从未见过一款富有数学元素的游戏，能够这么美

彭罗斯三角形，图片来源：GAOXIAOGIF.COM

我从未见过一款富有数学元素的游戏，能够这么美

纪念碑谷中的彭罗斯三角形
除了类似彭罗斯三角形的视觉错觉之外，还有一部分是利用“凹”与“凸”的错觉。因为“凹”与“凸”的相对明暗关系相同，因此人要依靠环境来判断究竟是凹还是凸。
3 |" j" S  {. O3 |

我从未见过一款富有数学元素的游戏，能够这么美

几个顶角是凹还是凸？
当然，说到不可能图形就一定要提到埃舍尔。
+ O- x/ r5 V% m9 e

我从未见过一款富有数学元素的游戏，能够这么美

早在二十世纪五十年代，荷兰画家埃舍尔就已经有了多幅表现视觉悖论的画作。他画得极其写实，因此造成的荒谬感就异常强烈。
在《纪念碑谷 2》中，萝尔的女儿独自乘船来到新大陆时，便遇到了这样一个谜题。
' E6 o$ \- l2 f. |" u6 M离开这个地方的门高高地挂在高塔上面，而破碎的路却不知通向何处，眼看着没有能帮助她升去高层的道具，殊不知沿着平面往前走，便已然到达了高层。
6 k) |- k8 {4 R

我从未见过一款富有数学元素的游戏，能够这么美

这副不可能的场景，在埃舍尔的作品《瀑布》中早有所体现。

我从未见过一款富有数学元素的游戏，能够这么美

埃舍尔《瀑布》（Waterfall, 1961），图片来自：http://www.mcescher.com/
! [. J2 q1 n1 s/ q# w. z这些悖论产生的原理都是相同的，即将三维物体投影到二维后产生的空间维度错觉。值得一提的是彭罗斯三角形在三维世界不可能存在，但在四维世界很容易就可以做到。正如莫比乌斯环、克莱因瓶。莫比乌斯环在二维世界不可能存在，需要在三维中扭曲；而克莱因瓶需要在四维扭曲，真正的克莱因瓶不存在交叉。
! {3 z- I) Q( ?( `等角投影，迅速建立空间印象 《纪念碑谷2》的谜题多是建立在立体空间的，而有的游戏的建筑其实十分复杂，如何保证让玩家尽可能快地接受信息，从而建立起空间印象呢？这里就用到了一个制图学经常用到的方法——等角投影。         
( V# X( Q7 R  [* f0 K" C: i简单来说，等角投影是一种在二维空间中呈现三维物体的一种方法，这种方法的特点是保证角度正确，但是会产生形变。
/ K1 M0 ~$ e6 `

我从未见过一款富有数学元素的游戏，能够这么美

彼得·艾森曼设计的Frank House等角投影图
$ q, ^: }/ H. j( b3 I+ ]最常见的应属墨卡托投影，这是制作地图普遍使用的投影方法。地球是一个球体，设想一个与地轴方向一致的与地球相切的圆柱，按照等角投影的方式把经纬线投到圆柱上。这样做的后果是越往两极，形变越大，拽得越开，但是点与点之间的长度比例都是正确的，即没有角度变形，但有严重的面积变形。把这个圆柱剪开，就形成了一张世界地图。也是因为严重的面积变形，本来很小的格陵兰岛因为靠近北极，地图上就变成了一个很大的岛。

我从未见过一款富有数学元素的游戏，能够这么美

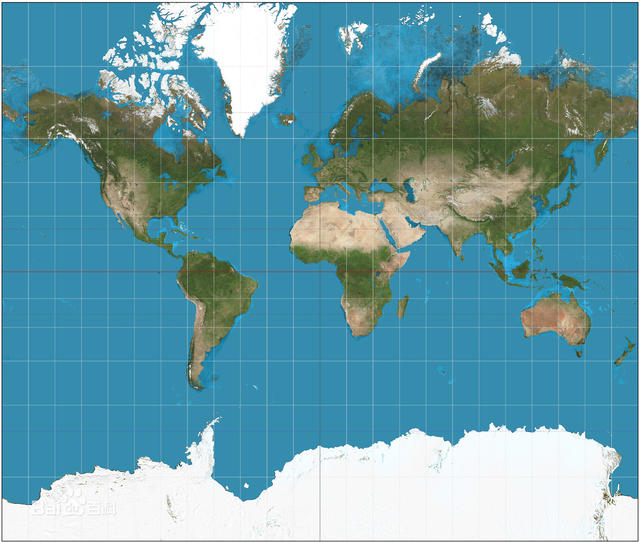墨卡托投影制作的世界地图，巨大的南极北极
当然了，《纪念碑谷2》运用的并不是墨卡托投影，而是建筑设计中更普遍的一种，将立体的建筑整个做了等角投影投射到画面上。正如上面所说的，这样做越靠近两端的地方就越会失真，仔细比对的话，《纪念碑谷2》的很多画面是不符合标准透视的，和地图一样，两头被拉大了。
《纪念碑谷2》透视VS真实透视，注意顶面底面，透视导致对边一定不平行
) n! a* ~" o1 V7 W% y这样的投影一定程度上克制了“近大远小”，使得本应是梯形的投影变成了长方形，于是就有了这样的魔幻效果：
5 E8 a, B7 [% `% ~3 f

我从未见过一款富有数学元素的游戏，能够这么美

+ p: k/ L, {+ w% v) G1 e+ A但是这种有限的失真换取的是更加精确的表面与内部的视觉。因此玩家可以迅速建立空间影像帮助了解这个世界。
1 h$ R4 k' g( V0 d旋转对称与轴对称，手残也能画好符 《纪念碑谷2》的不同于一代的另一个巧妙设计是关卡之后通关的图形可以自己画。很多人甚至会为了画好这个图形重新打好几遍那个关卡。然而并不是所有人都是大触，《纪念碑谷2》怎样有信心把这样一个任务交给可能手残的玩家呢？这里就用到了大家都知道的旋转对称与轴对称。
, c5 f+ u5 H0 X' v, I8 j. L

我从未见过一款富有数学元素的游戏，能够这么美

哪怕单独的一个很丑很丑，线条仿佛触电抽搐，图形诡异，在对称成一圈之后就会变得和谐。就如同小的时候剪窗花，把红纸叠成好多叠，然后乱剪一通，打开看也依然赏心悦目。
- X) W! }+ Y+ l% ]+ v6 g. f旋转之所以能拥有这样的魔力，是因为它把你的瑕疵多次按照规律重复，这样瑕疵本身拥有了规律，成为了一种秩序所在。并且它与图案的剩下部分拥有同步的规律，也就可以融合进图形，即使你手残也可以放心大胆地画。
别看程序自动帮你轴对称很容易，现实生活中要想画出对称的事物其实很困难。不说复杂的花，单是正多边形的尺规作图，就要让数学学者们琢磨好一阵子。
尺规作图，是指用没有刻线的直尺与圆规作图。在所有有关正多边形尺规作图的故事当中，天才数学家高斯发明正十七边形作图方法是最有名的了。

我从未见过一款富有数学元素的游戏，能够这么美

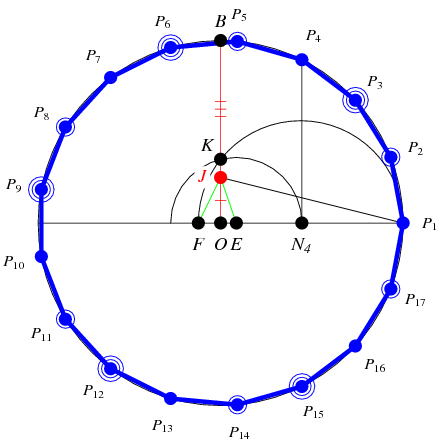正十七边形尺规作图方法
; z3 I2 W; i( ^. N. }& t当然，这只是个传说，这个方法并不是高斯发现的，但是高斯确实在尺规作图领域有很大贡献，他证明了有哪些多边形可以被尺规作图——当且仅当边数是费马素数或者两个不同的费马素数的乘积，或者是这些数的2的乘幂倍时。
; P1 y% o+ a- `根据高斯的理论，正65537边形（内角和为11796300°，对角线2147450879条，没错我不是在搓键盘）可以被尺规作图。德国数学家Johann Gustav Hermes花费了10年给出了具体的作法并于1894年发表。这是人类给出的最多条边的多边形作图方法。
0 |8 t( F, K& ^( T1 B& i

我从未见过一款富有数学元素的游戏，能够这么美

坐标轴中间已经看不见的小点点就是正65537边形
如何成就点睛之笔？ 《纪念碑谷2》最亮眼的亮点当属树的设计。在游戏中，树在光的照耀下就回成长，离开光会缩回，担当了动态机关的同时，带来的美感令人惊艳，这种美除了树与光本身之外，还来源于对比和跳脱。
《纪念碑谷2》的背景环境与一代一样多为几何形建筑，色彩都是“冰淇淋色”。即饱和度适中，不含高光，不贴材质，一切都以纯色呈现。另外建筑多为规则图形，且参考了建筑的解构主义与极简主义，线条规则清晰，几何美突出。

我从未见过一款富有数学元素的游戏，能够这么美

西班牙红墙，图片来自：Ricardo Bofill
* ^4 c" ^# x7 x. P! Y! X4 C而这棵树就不一样了，饱和度通常偏高的颜色，形状没有完全抽象成纯色立方体，而是略微写实地有了一些材质和不规则图形（树叶、树干）。且因为关卡设计，树在游戏中是即时变化的，这都和直来直去的背景形成了对比。
7 U; M( B% G/ N' N

我从未见过一款富有数学元素的游戏，能够这么美

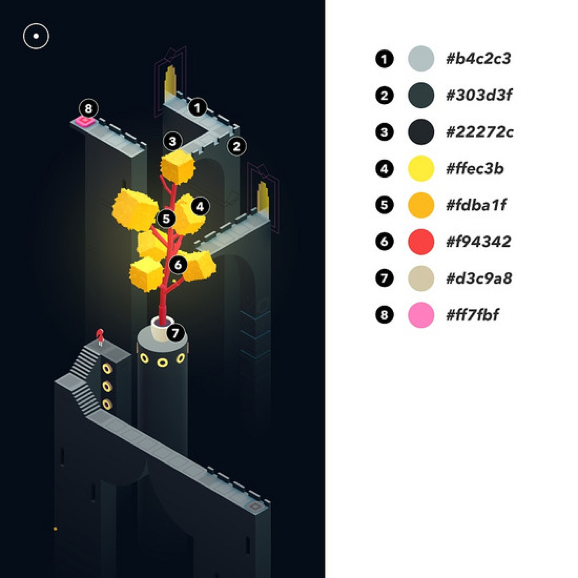色彩对比，图片来自：http://www.tuicool.com/

我从未见过一款富有数学元素的游戏，能够这么美

即时变化的树
这样的对比让树成为了整个画面的点睛之笔，在视觉上有一个跳脱的点，让这个场景显得生机勃勃。
) S* P/ F1 t; p: l2 Y  n6 q, Z( t除了颜值担当之外，树还有一个独特的象征，它象征着女儿的成长与蜕变。走到果园的尽头，女儿走进树屋，树木随即生长，等到再次见到光明重新绽放之时，长大成人的女儿站在树的顶端，重新打量这个世界。在这个成长的故事里，处处阳光普照。

我从未见过一款富有数学元素的游戏，能够这么美

: L% D) g6 U8 G! x0 Z巧妙地运用数学让画面更加协调，达到应有的视觉效果，无形中给这个游戏加分不少。如果你在寻找一个没有负担轻松温馨，但同时充满惊喜、挑战常识的冒险，那么《纪念碑谷2》将是一个完美的选择。
如果你已经玩过这款游戏了，那么我想你一定已经感受到《纪念碑谷 2》中数学元素所带给你的迷幻、神秘和优雅了。
. T3 e3 v: {' }. K6 O& H( z" z如果你还没有玩过，那么我想你正需要这款游戏，来带你摆脱对数学的偏见，感受到数学之美。

xmeve

正打算玩起来

来自APP客户端