想追她？先算算你要等多久

余急皿

一个女孩从第一次被人追求到结婚，平均会有多少人去追她？她又会谈几次恋爱？其实，我们可以建立一个简化的模型估算出来。
% Q/ \6 V6 J+ I7 J4 O

/gkimage/oy/fl/0q/oyfl0q.png

这是一个等待和处理的过程不妨假设，一个条件不差的女孩，始终会有人追（被追求频率不同而已）。如果把追求者看成一个列队，当追求者出现时，就可被看成一个“请求”放到这个列队里。对于女孩来说，要“处理”这个“请求”，她无非有两种选择：接受或者拒绝（这里不考虑其他的复杂行为）。而一旦她开始处理某个请求，结局只有两个：

1. 
   % B. H- Y, t+ b/ P
2. 女孩和他谈恋爱直到分手（或者结婚）
   
3. 
   
4. 女孩经过或短或长时间的考虑后明确拒绝追求者
   

复制代码

分手或完成拒绝意味着完成处理，这是就把他从列队里除去。女孩和这个人谈恋爱所经历的时间，或者决定拒绝所用的时间叫作“处理时间”；某个人从成为她的追求者直到分手或被拒绝的时间则叫作“等待时间”。那到底平均有多少人在女孩的列队里？平均每个人要在女孩的列队里等多久？
简化成数学模型平均来看，对某一个女孩子来说，追求者出现频率可当作是随机的，那两个追求者出现的时间间隔就可以用指数分布来表示。因此追求者出现的频率就服从泊松分布。另一方面，由于追求者的出现是随机的，女孩子心仪的对象就是随机出现的，这导致了女孩谈恋爱的时间是随机的，即其处理时间服从指数分布，女孩在一段时间内谈恋爱的频率也就服从泊松分布。
# R0 w2 K6 u5 |7 J+ f为了将实际复杂的问题进行简化，我们做出下面几条理想化的假设：
（1）追求者都是死心眼，一旦成了追求者就不会放弃，一直待在列队里，直到分手或者被拒绝。也就是说当列队中的对象没有被处理时，他就会排队等待处理。
（2）女孩不会脚踏两只船，每次最多只和一个人谈恋爱（每次只处理一个请求）。
（3）当女孩正在处理一个请求时，设其他追求者有绅士风度，不会骚扰她。
（4）女孩处理列队里的请求时遵循先到先谈（First Come First Serve, FCFS）原则，遇到靠谱的就恋爱，遇到不靠谱的就拒绝，决定拒绝某人可能要经历一定时间。
既然追求者出现的时间间隔和处理时间都服从指数分布，我们就分别用 a(t) 和 b(t) 表示二者的密度方程（density function）：

/gkimage/j6/o3/o7/j6o3o7.png

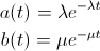根据泊松分布的特性我们可以知道：追求者出现的时间间隔的平均值是 1/λ，处理时间的平均值是 1/μ， λ 指追求者出现的频率，μ 指的是女孩处理请求的频率 。
用排队论算出追求者平均等待时间当追求者超过 1 个时，就会形成排队的状态，这时候我们可以引入马尔可夫链（Markov Chains）来分析这个问题：

/gkimage/wa/q1/x6/waq1x6.png

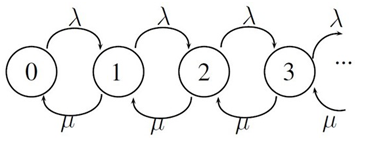在上图中，每个圆圈代表排队系统的一个状态，其中的数字代表列队长度：当前追求者个数。在每个状态，每来一个追求者，系统就到了下一个状态（追求者的人数加 1），女孩谈完一次恋爱或者拒绝一个人，系统就回到了上一个状态（追求者的人数减 1，因为某个追求者被拒或者成了前男友）。
# q0 \% e+ O$ d8 r+ X; S) X) u  O# a用 p n 表示系统处于状态 n（姑娘的列队里有 n 个追求者）的概率，系统要达到一个稳定状态，必须要满足下面的递归方程：
9 M" w% f9 W3 j$ f

/gkimage/83/5z/ar/835zar.png

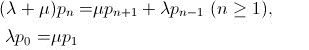通过迭代法解这个等式，可以得出 p n 的表达式：

/gkimage/z8/na/mn/z8namn.png

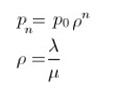另外注意到，对于这条马尔可夫链来说，各个状态的概率和应当为 1（因为包含了所有情况）： p 0 + p 1 + ... + p n = 1 。结合上式，最终解得：
* \0 f) c% j" y, u! O7 I- y

/gkimage/e5/z2/hr/e5z2hr.png

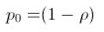有了概率，我们就可以计算追求者列队的平均长度了。随机变量 N 代表列队在稳定状态时追求者的数量，根据期望：

/gkimage/wx/6k/hr/wx6khr.png

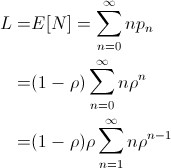化简可得：
" ]: E# _0 d! U: ?$ C

/gkimage/ek/hb/te/ekhbte.png

/gkimage/a3/pn/a1/a3pna1.png

知道了这个女孩的追求者数量的期望值，我们还想知道平均每个追求者要等多久。为了解决这个小问题，我们得用排队论 (queueing theory）的 Little's formulas：

/gkimage/27/28/on/2728on.png

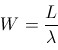W 就是追求者的平均等待时间（从进入列队到和女孩分手或被拒绝），结合上面的结果，不难得出：
* d, n, n$ H' h0 m( Q, p

/gkimage/1h/zh/f5/1hzhf5.png

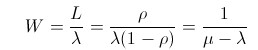用结论估计现实公式已经推出，理论的武器已经牢牢握在手里，剩下的事情就是想办法了解女孩的历史，得到两个关键数据： λ 和 μ。追求者出现的频率取决于女孩的抢手程度，而她恋爱的频率，大致也就等于她谈过恋爱的次数和女孩从开始被追到现在的时间的商。例如，一个女孩子，每个月都会有一个人来追求她，而她每半年谈一次恋爱，这里的半年，是指女孩从上一次恋爱分手到这次恋爱的时间，这个周期女孩处理的请求数平均是 7。那么追求者的平均等待时间就是 1 / （7 / 6 - 1 / 1） = 6 ,追求者的平均等待时间是 6 个月。但是会有多少人花半年时间等一个展示自己的机会呢？要注意的注意，这里等来的不过是请求被处理，也就是女孩对你的注意，说不定 12 个月的等待到头来的结果还是被拒绝。所以从这里我们可以看到，默默等待被心上人青睐的成本，那还是相当大的。这或许就是情痴濒危的原因了吧。
7 Y* W! O6 Q7 O) w" g另一方面，假设女孩的恋爱频率是相同的，越抢手的（通常也就是越漂亮的）女孩，追求者出现的频率 λ 就会越大，因此 W 的值就会越大。这就说明，想用真心和等待默默打动“热门”女孩，成功概率实在不高。如果真想追，那倒不如“舍得一身剐，敢把皇帝拉下马”，就算她在谈恋爱中，也采取实际行动。
有趣的是，这项“研究成果”对女孩也是有用的。女孩把自己的数据代到公式里算出自己的追求者平均要追求多久，紧接着就能算出自己在某一段时间里能遇到多少个追求者。例如，女孩经过计算得出追求者的平均等待时间是两个月，那在她 16 岁到 26 岁这十年的黄金时间里，遇到的追求者数量的期望就是 60 个。想挑个好老公，女孩心里要有数才行。按数学家的建议，那就应该 先拒绝掉前面 37% 的人 ，再逐个考察，静候下一个比这些人都好的人。
关于模型的两点说明虽然我们用这个数学结论指导爱情，但要注意的是，现实情况并没有如此理想化。在这里有两点需要说明。首先在模型假设里，我们假设追求者一旦进入队列就不会自动离开，但通常在一段时间女孩没有反应后，多数人会知难而退自动离开，并不会等那么久，尤其是看到女孩已经谈恋爱时。
( H* h8 u  g! n2 T- v4 G9 X另一方面，女孩每次只能处理一个请求。一次只和一个人谈恋爱是常见的，但在此之外，同时间考察和拒绝若干追求者也是正常的（而不是模型中那样假设的每次拒绝一个人）。现实中，对很多追求者来说，几乎都是直接被忽视掉。从这个角度讲，处理请求的频率 μ 通常大于请求到来的频率 λ（因为短时间内就可以拒绝很多人），这一点与模型项符。
+ W1 G" T/ D( M! ?实际上，这个模型最适用的是，会让女孩动心的追求者队列（这样的追求者不多，相应的 λ 就不会很高）。这个队列不会太长，因为让女孩动心的追求者很少会同一时间出现很多个。而要拒绝任意一个这样的追求者，都需要仔细考虑一段时间才能下决心。
0 l- I5 Y3 F& [1 P0 t" v编辑的话虽然是个很理想化的模型，但还是比亲自去问她，得到的答案要准确多了吧。不过与其苦等，不如 找一款合适自己的理工女 ，再 用个浪漫的约会方案 俘获她的心。
9 }% u5 R1 f. ~0 ]参考资料：
2 m6 D& |8 k  @/ ^$ l[1] Fundamentals of Queueing Theory 4th edition, 2008
  a2 I: V5 c8 J: l[2] 维基百科： Poisson distribution
[3] 维基百科： Markov chain

smallluyan

宅女表示。。。我有话但是我不想说。。。。黯然飘过。。。。。。。。。

223311

概率论总能被死理性派弄得有趣起来。