尼斯湖水怪荡起的那一圈涟漪

幸福时刻

英国的“尼斯湖水怪”绝对是一个流传了很多年的传说，不过它真正“走红”是从1934年的4月开始的。伦敦医生威尔逊自称，当他走在尼斯湖岸边一条小路上时候，突然看到150码到200码之外（137-183米）的远方有一个奇怪的巨大动物浮出水面。他立刻拿出随身携带的照相机，抓拍了一张水怪照片，第一次以图像的形式记录下了这个传闻已久的水怪的形象。照片被一家报纸刊出后，立刻引起了轰动。
从此，关于尼斯湖水怪目击事件、照片、录像、考察热潮一阵高过一阵，每年来尼斯湖的游客络绎不绝。尼斯湖水怪的吸引力经久不衰，而在其他各国的江河湖海中，山寨版的尼斯湖水怪也纷纷出现。

/gkimage/gq/ni/78/gqni78.png

威尔逊医生拍摄的水怪照片。

/gkimage/wo/bc/to/wobcto.png

放大的照片。
对于照片中的动物，当时很多人认为这货不会是已知的任何水生生物，而很有可能是身长可以达到十几米、已经灭绝的恐龙——蛇颈龙。这张照片相当有名，甚至连漫画《哆啦A梦》里都有它的身影。不过在漫画中，解释的还并不是那么详细。

/gkimage/fl/8w/pf/fl8wpf.png

《哆啦A梦》第六卷。
# o( ^3 K, W1 H1 T- {: m4 X' D3 _4 e椭圆的水波在照片发布后的几十年，尽管对于这张照片中的生物争论不休，意见各异，却很少有人科学地研究过这张照片本身的真假。直到1982年，英国一位名为斯图尔特?坎贝尔（Steuart Campbell）的科普作家在《英国摄影期刊》用简单的计算指出了照片中的破绽。
7 A& E+ O5 B% Q6 Y令人感到意外的是，破绽并非来自于水怪本身，而是出在了水怪周围荡起了那几圈涟漪之中。涟漪是由振动产生的，无论是水怪突然从水里钻出来透透气，还是把一块石头扔到水里，都会让水上下地振动，产生一个振动的中心。随后这个振动会以水波的形式向各个方向传递，由于传递的速度相等，所以形成的水波形状一定是圆形的。
) i( }2 I+ J3 y1 W4 v  }) Z

/gkimage/m2/tg/en/m2tgen.png

水波的传播速度相等。
可是看一下上面这幅水波的照片，它们无一例外都是椭圆形的，这如何解释呢？如果在拍摄的时候，把照相机伸到水波的正上方，让照相机镜面和水面平行，那么拍到的水波一定是圆形。可是大多数时候，拍摄者都是在一旁从侧面的角度拍摄水波，由于“近大远小”的关系，圆形的水波在照片里就会被扭曲成椭圆形的形状。在尼斯湖水怪的照片里也不例外，仔细观察一下会发现，水怪周围的水波形状也是椭圆形的。
这椭圆的具体形状，里面隐含了一条重要的信息：拍摄的时候照相机向下倾斜的角度是多少。如果角度很小，椭圆的形状就会很扁，如果角度很大，甚至达到了刚刚所说的与水面平行的90度，那么照片里圆形的形状就会依旧很圆，被扭曲地很轻。
根据尼斯湖水怪的那张照片，按照下图的方法，我们可以从水的涟漪中推算出当时这位医生是把照相机向下倾斜了18度，对准水怪拍到的照片。

/gkimage/sy/pf/1z/sypf1z.png

/gkimage/yp/gr/y6/ypgry6.png

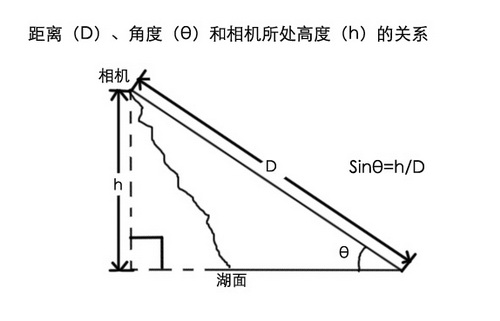通过椭圆形状和距离计算高度。
7 b; A) M4 U* ~/ Y1 Y; x你到底站在哪里拍的？具体的角度一出，问题就来了：这位医生说水怪当时距离他有130米以上，从这个距离和18.8度的角度，可以推知他所站的地方离水面的高度应该有40米以上。可是坎贝尔根据这位医生当时的描述的位置，找到了那一段湖边小路位置的地图资料，并实地做了探访。发现那一段路在前后几公里范围内的最多能找到几个距离湖面30米高的位置，大多数的位置只有十几米、二十几米高，如果医生是在这些位置拍的照片，恐怕当时怪物离他的距离只有数十米，与他所说的的距离有很大出入。
5 S2 }+ H  r- [- M3 F/ f" {为了确定医生到底是在哪里拍的照片，Campbell又对照片从另一个角度做了分析。首先，他确定了图片中的三条基线：
4 ~3 F4 P1 ]6 |2 d9 x$ p

/gkimage/34/lo/xk/34loxk.png

整张照片最上面很小的部分是湖的对岸（红线）在照片的底部看不到湖岸的这一边任何岩石和沙滩（绿线）水怪在照片中处于中间稍微偏下的位置（蓝线）你可能会说，这些东西是个人都能看出来，又怎么样呢？
尼斯湖的面积虽不算很大，但岸宽也有2.4公里。红线可以近似看作是地平线，在自己的水平正前方。上面照片里的红线相当于下面这张几何图里的红点，蓝线相当于下面这张图的蓝点，绿线相当于下面这张图中的绿点。下图中的三条会聚到一起的线分别表示从三个点到照相机的光线。
通过上面的计算可知，照相机是向下倾斜18.8度对准水怪的，所以这张几何图里的红点光线和蓝点光线之间的夹角就是18.8度。又因为在水怪照片里，红线和蓝线间的距离与蓝线与绿线间的距离相差不大，也就意味着在几何图里，蓝点的光线和绿点的光线之间的夹角应该略小于18度，这样红点的光线和绿点的光线之间的夹角估计有36度。
既然在照片里医生所在的湖的这一侧的岸边没有任何景物照进照片里，这就要求岸边的位置比较陡，角度要大于36度才可以。如果岸边不够陡的话，那水边的岩石和绵绵延延的沙滩，一定会有东西进入到照相机36度的视野。

/gkimage/h5/bk/4n/h5bk4n.png

通过三条基线计算高度。
) j/ O2 y8 f; p4 F坎贝尔再次研究了那一段路的地形，根本没有发现这么一个陡峭的位置，让照片里只有“彼岸”，没有“此岸”。他所能找到的最可能的地方是岸边一个10米高的地方，可是按照10米的高度和18.8度的角度，水怪距离岸边的距离只有30多米。如果是这样的话，只能说那位医生摄影师的眼神也未免太差一点的吧，把30米远的东西当成了150米远的东西。照片计算出来的结果和本人的描述大不相符，这位医生恐怕不是伪造了照片，就是说了谎话。
就算是摄影师的远近方位感不太好，进一步算下去，可以算出图中红点和绿点的距离，也就是照片中红线和绿线的间距所对应的实际距离，结果是大约20米。在照片里，水怪的高度只占了其中的3.6%，这样一算，最后20乘以3.6%，水怪高度只有70厘米而已，这个身高标准是小萝莉级别的，哪里是蛇颈龙一类怪物的标准。论文作者坎贝尔推测，照片里的动物也就是一只翘着尾巴的水獭而已。
0 |7 n+ s3 X3 f3 p' T' }没过几年，坎贝尔对照片的福尔摩斯式地质疑得到了应验。照片的始作俑者威尔逊医生一直活到1994年90岁高龄时候去世，在临终前说出了照片的真相：他当时在尼斯湖岸边根本没有看到水怪，这张照片是他用玩具潜水艇模型拍摄的。

在漫画故事里，尽管照片被证明为假，不过水怪还是被多啦美找了过来~

慕容决飞

尼斯湖是苏格兰五日游必去景点之一,这老头一张照片,这么多年来拉动了多少当地旅游..

richard320

原来是假的啊.................以前老陪外公看走进科学，老讲这个...........讲了一遍又一遍.............还木有结果.........坑爹啊！！

苏Fseries

大概看到别人几乎是被自己玩弄的样子有一种快感吧……