埃舍尔威武！解读瀑布上的两个立体图形

enur123456

/gkimage/nb/xt/f4/nbxtf4.png

上面这张图想必大家已经看过无数多次了吧。没错，这正是天才画家埃舍尔（M. C. Escher）的名画《瀑布》。画中的瀑布把从古至今各种物理规律统统蹂躏了一遍，但各处细节看上去又是如此天衣无缝，实在让人称奇。
1 X  Y) i6 J) C4 \: w1 F. r果壳网 DIY 站 的驻站编辑天蓝提琴纯手工打造了《瀑布》一画中的 瀑布实体模型 ，令人叹为观止。本人专程前往天蓝提琴的工作室膜拜真实版的瀑布，震撼得瞠目结舌，佩服得五体投地。想看看天蓝提琴如何把不可能图形搬到现实的，请点击 此处 穿越到果壳网 DIY 站。
同时，我也第一次看到了《瀑布》中两个立体图形的真身，把它拿在手里 360 度看了个遍；随后在各大网站上搜索有关的资料，终于解答了困扰我已久的疑问。现在就来仔细给大家讲讲，这两个立体图形到底是什么。
% M& n. V6 i$ S# g3 w6 x& \, i三立方体合体

/gkimage/yu/te/ar/yutear.png

/gkimage/v6/b0/59/v6b059.png

左边的那个立体图形叫做“三立方体合体”（compound of three cubes），它的 360 度高清无码动画如上图所示。我们列举一些与这个立体图形有关的一些事实。

它的构造方法：想象完全重合的三个立方体，然后把这三个立方体分别绕着 x 轴、y 轴、z 轴旋转 45 度，便可得到这个高度对称的三立方体合体。        三个立方体总共有 24 个顶点，它们的坐标就是 (±√2，0，±1) 及其所有排列。

/gkimage/an/wf/kl/anwfkl.png

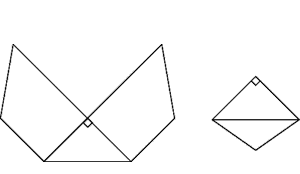
只需要用上面两种形状的纸片各 24 个便可粘合出这个立体图形。据此还可以算出，整个图形的表面积为 72 - 45√2 ≈ 8.36（假设每个立方体的边长为 1）。        这三个立方体的公共部分是一个 18 面体，其中 6 个面是正方形，另外 12 个面是六边形。        这三个立方体相交后一共分割出了 67 个区域。三个立方体是否还能切出更多的区域，仍是一个未解之谜。
3 {. I0 S( G. f4 x$ V

埃舍尔多面体

/gkimage/np/70/62/np7062.png

/gkimage/0h/0i/1q/0h0i1q.png

右边那个立体图形可以说是埃舍尔的原创几何图形了，在这之前它并没有一个固定的名字。因此，后来人们就把这个图形直接叫做了“埃舍尔多面体”（Escher's solid）。我们也来看一看这个多面体的秘密：

它是一个菱形十二面体（每个面都是菱形的十二面体）对应的星状多面体，即在菱形十二面体的每个面上“长”出一个四棱锥得到的图形。        它可以用八个相同的小八面体粘合而成。        它还可以看作是由三个完全相同的大八面体相交组合而成的。        很难想象，单用埃舍尔多面体，可以既无重复又无遗漏地填满整个空间！
. P& g9 {" s1 L; K+ r

埃舍尔非常喜欢在自己的作品中添加各式各样的立体图形。在埃舍尔的作品《星星》（Stars）中，他更是把多面体之美表现到了极致。最后，不妨就用这幅图来结束这个永远也讲不完的话题吧。

/gkimage/32/rm/sz/32rmsz.png

luckylake

赞美，作为一个矿物爱好者，表示看见了各种晶体和双晶……

baoyang

我在想的是瀑布的流向，即是从上往下，又是从下往上